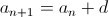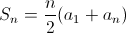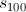12.1 (cont.) - Introduction to Limits

Properties of Limits:
Let b and c be real numbers and let n be a positive integer.












Operations with Limits:
Let b and c be real numbers, let n be a positive integer, and let f and g be functions with the following limits:
1. Scalar multiple:





2. Sum or difference:




3. Product:




4. Quotient:





5. Power:




Direct Substitution:
You have seen that sometimes the limit of f(x) as x approaches c is simply f(c). In such cases, it is said that the limit can be evaluated by direct substitution.Finding the limit using direct substitution is fairly easy. Just plug the c-value into the function and then solve using simple algebra skills.

Continuity:
A graph is discontinuous if there are any:
- holes
- asymptotes
- breaks
Here, f is continuous at a.

T or F?
If...




then f is continuous at a.

This is FALSE.
This proves that there is in fact a limit, but it's not for certain that the graph is continuous.

Introduction to Limits-12.1

Notation for Limits

lim f(x)=L
xa


As x gets arbitrarily close to a, y gets arbitrarily close to L


Example
f(x)= 2x-3
lim f(x) = 1
x 2


There are three cases when a limit does not exist:
1) When the right hand and the left hand do not approach the same number
2)When there is an asymptote 
3) * when the graph is oscillating between 2 numbers very quickly
  * this case is very rare

BINOMIAL THEOREM!!!!

PASCALS TRIANGLE-

Each row in the triangle begins and ends with 1. Each element in the triangle is the sum of the two elements immediately above it.

If a diagonal of numbers of any length is selected starting at any of the 1's bordering the sides of the triangle and ending on any number inside the triangle on that diagonal, the sum of the numbers inside the selection is equal to the number below the end of the selection that is not on the same diagonal itself.

______________________________________________________

EXPANDING BINOMIALS-

Equations:

Help:

(x+y)⁰ = 1

(x+y)¹ = x + y
(x+y)² = x² + 2xy + y²
(x+y)³ = x³ + 3x²y + 3xy² + y³
(x+y)⁴ = x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴
(x+y)⁵ = x⁵ + 5x⁴y + 10x³y² +10x²y³ + 5xy⁴ + y⁵

There are several things that you hopefully have noticed after looking at the expansion

• There are n+1 terms in the expansion of (x+y)ⁿ
• The degree of each term is n
• The powers on x begin with n and decrease to 0
• The powers on y begin with 0 and increase to n
• The coefficients are symmetric

Example:

Expand (x+2)^5

Let a = x, b = 2, n = 5 and substitute. (Do not substitute a value fork.)

EXAMPLE 2:

Find the coefficient of the x64 term : (5x-2i)^7

7C4= 35

nCr=35

a=(5x)^4

b=(-2i)^3

note: the exponent of a and b have to equal 7

(35) * (5x)^4 * (-2i)^3= -175,000(x^4)(i^3)

(35) * (5x)^4 * (-2i)^3= -175,000(x^4)(-i)

(35) * (5x)^4 * (-2i)^3= 175,000(x^4)i

(35) * (5x)^4 * (-2i)^3= 175,000i <--take out the x^4 because it only asked for the coefficent

=175,000i

VIDEO HELP!

1. http://http://www.khanacademy.org/video/binomial-theorem--part-1?playlist=Precalculus

-Introducing raising (a+b)^n

2. http://www.khanacademy.org/video/binomial-theorem--part-2?playlist=Precalculus

-Pascals triangle, Expansion

3. http://www.khanacademy.org/video/binomial-theorem--part-3?playlist=Precalculus

-Combinations

Geometric Sequences

Geometric Sequences- unlike arithmetic, geometric sequences are repeated multiplication.

ex.) 3, 6, 12, 24, 48, 96,...

3(2)=6, 6(2)=12, 12(2)=42, . . .

r = 2

(r) is the common ratio and r CANNOT equal zero

Geometric Partial Sum

~Take the first equation and multiply it by (r) to get the second equation

~ Subtract the two equations, cancel out like terms to end with:

~ Take out an Sn out from the left side and a1 from the right side so you end up with:

~divide both sides by (1-r) to get the final equation:

EX.) Let an be geometric sequence with a3 = 12 and a6 = 96. Find the 10th partial sum.

To find (r), first find the difference between n;

a6-a3= 3

3 becomes the power of r which equals the fraction of two terms.

take the cube root of 8

r= 2

Plug numbers into the partial sum formula

r= 2

a1= 3

n=10

Infinite Sum

Arithmetic Sequences (9.2)

Arithmetic Sequence: a sequence whose consecutive terms have a common difference

Example:

3, 6, 9, 12, 15, 18, ...

6-3=3, 9-6=3, 12-9=3, etc. The common differnce here is 3

The common difference is represented by d.

The Recursive Formula

Example:

Find the next term in the sequence

3, 6, 9, 12, 15, 18, __

=18, d=3

= 18+3

= 21

The nth Term of an Arithmetic Sequence

Where

Now, since Mr. Wilhelm doesn't like this formula, we can do this:

Start With:

Replace c:

Simplify:

Example:

Find the 10th term.

3, 6, 9, 12, 15, 18, ...

d=3

=3

Formula:

=3(10-1)+3

=30

Sum of Finite Arithmetic Sequence

How it came to be:

Find the sum of all numbers 1-100

=1+2+3+...+98+99+100 Add the first set of numbers to a reverse set of the same numbers

=100+99+98+...3+2+1

=101,101,101,...,101,101,101 All answers are 101 and the sum is doubled

=100(101) Multiply answer by total number of numbers in sequence

=10100/2 Divide by 2 so you get rid of the doubled sum

=5050 ANSWER!

Example:

Find the sume of the sequence:

3, 6, 9, 12, 15, 18

=3

=18

n=6

=63