Arithmetic Sequence: a sequence whose consecutive terms have a common difference
Example:
3, 6, 9, 12, 15, 18, ...
6-3=3, 9-6=3, 12-9=3, etc. The common differnce here is 3
The common difference is represented by d.
The Recursive Formula
Example:
Find the next term in the sequence
3, 6, 9, 12, 15, 18, __
The nth Term of an Arithmetic Sequence
Now, since Mr. Wilhelm doesn't like this formula, we can do this:
Example:
Find the 10th term.
3, 6, 9, 12, 15, 18, ...
d=3
=3(10-1)+3
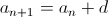











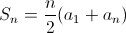









No comments:
Post a Comment